Ecuații ecuații egale - exemple cu soluții, singularități și formule
În societatea modernă, capacitatea de a efectua acțiuni cu ecuații care conțin o variabilă pătrată poate fi utilă în multe domenii de activitate și este utilizată pe scară largă în practică în dezvoltarea științifică și tehnică. Dovada acestui lucru poate servi drept proiectarea navelor maritime, fluviale, rachetelor și a aeronavelor. Cu ajutorul acestor calcule se determină traiectoriile mișcării diferitelor corpuri, inclusiv obiectele cosmice. Exemplele cu soluția de ecuații patratice găsesc aplicații nu numai în prognozarea economică, în proiectarea și construcția clădirilor, dar și în cele mai obișnuite condiții de zi cu zi. Acestea pot fi necesare în drumeții, în sport, în magazine atunci când fac cumpărături și în alte situații foarte frecvente.
conținut
- Am împărțit expresia în factori componenți
- Exemplu
- Extinderea expresiei în multiplicatori
- Extragerea rădăcinii pătrată
- Calcularea parcelei de teren
- Discriminantă
- Despre rădăcini și formula lor
- Exemple și sarcini
- Teorema lui vieta
- Graficul și ecuația parabolică
- Intersecția ramurilor parabolice cu axa abscisa
- Din istorie

Am împărțit expresia în factori componenți
Gradul ecuației este determinat de valoarea maximă a gradului y al variabilei pe care expresia dată o conține. În cazul în care este egal cu 2, atunci o astfel de ecuație se numește quadratic.
Dacă se vorbește limba formulelor, atunci aceste expresii, oricare ar arăta ele, pot fi întotdeauna reduse la forma atunci când partea stângă a expresiei este formată din trei termeni. Printre ei: topor2 (Adică variabilă, construită în pătrat cu raportul său), bx (necunoscute fără pătrat cu coeficientul său) și c (componenta liberă, adică numărul obișnuit). Toate acestea în partea dreaptă sunt egale cu 0. În cazul în care un astfel de polinom nu conține unul dintre termenii săi constituenți, cu excepția axului2, se numește o ecuație parțială incompletă. Exemple cu rezolvarea unor astfel de probleme, importanța variabilelor în care este ușor de găsit, ar trebui să fie luate în considerare mai întâi.
Dacă expresia arată astfel în așa fel încât termenii din partea dreaptă a expresiei să aibă două, mai precis topor2 și bx, este mai ușor să găsești x luând variabila din paranteze. Acum ecuația noastră va arăta astfel: x (ax + b). În plus, devine evident că fie x = 0, fie problema reduce la găsirea unei variabile din următoarea expresie: ax + b = 0. Aceasta este dictată de una dintre proprietățile multiplicării. Regula spune că produsul a doi factori dă 0 ca rezultat numai dacă unul dintre ei este zero.
exemplu
8x2 - 3x = 0
x (8x - 3) = 0
Procedăm conform regulii descrise.
x = 0 sau 8x - 3 = 0
Ca rezultat, obținem două rădăcini ale ecuației: 0 și 0,375.
Ecuațiile de acest fel pot descrie deplasarea corpurilor sub acțiunea gravitației, pornind de la un anumit punct luat ca origine. Aici notația matematică are următoarea formă: y = v0t + gt2/ 2. Înlocuind valorile necesare, echivalând partea dreaptă a lui 0 și găsind necunoscute, se poate afla timpul care trece de la momentul ridicării corpului până în momentul căderii sale, precum și multe alte cantități. Dar vom vorbi despre asta mai târziu.

Extinderea expresiei în multiplicatori
Norma descrisă mai sus permite rezolvarea acestor probleme în cazuri mai complicate. Să luăm în considerare exemplele cu soluția de ecuații patratice de acest tip.
X2 - 33x + 200 = 0
Acest trinomial patrat este complet. În primul rând, transformăm expresia și extindem-o în multiplicatori. Există două dintre acestea: (x-8) și (x-25) = 0. Ca rezultat, avem două rădăcini 8 și 25.
Exemplele cu soluția de ecuații patratice din clasa a IX-a permit acestei metode să găsească o variabilă în expresiile nu numai celei de a doua, dar și a celei de-a treia și a patra ordine.
De exemplu: 2x3 + 2x2 - 18x - 18 = 0. Când descompuneți partea dreaptă în factori cu o variabilă, obțineți trei, adică (x + 1), (x-3) și (x + 3).
Ca rezultat, devine evident că această ecuație are trei rădăcini: -3- -1-3.
Extragerea rădăcinii pătrată
Un alt caz al unei ecuații incomplete de ordinul doi este o expresie în limba literelor reprezentată astfel încât partea dreaptă să fie construită din componentele axei2 și c. Aici, pentru a obține valoarea variabilei, termenul liber este transferat în partea dreaptă și apoi se extrage o rădăcină pătrată din ambele părți ale egalității. Trebuie remarcat că în acest caz rădăcinile ecuației sunt de obicei două. Excepțiile sunt doar egalități care nu conțin deloc termenul c, unde variabila este zero, precum și variante de expresii, atunci când partea dreaptă se dovedește a fi negativă. În ultimul caz, nu există soluții, deoarece acțiunile de mai sus nu pot fi efectuate cu rădăcini. Trebuie luate în considerare exemple de soluții de ecuații patratice de acest tip.
3x2- 48 = 0
3x2 = 48
În acest caz, rădăcinile ecuației sunt numerele -4 și 4.
Calcularea parcelei de teren
Nevoia de astfel de calcule a apărut în cele mai vechi timpuri, deoarece dezvoltarea matematicii în multe privințe în acele timpuri îndepărtate sa datorat necesității de a determina cu cea mai mare precizie zonele și perimetrele pământului.

Exemple de soluție de ecuații pătratice, compilate pe baza acestui tip de probleme ar trebui să fie luate în considerare și noi.
Deci, să presupunem că există o bucată de pământ dreptunghiulară, a cărei lungime este cu 16 metri mai mare decât lățimea. Este necesar să se găsească lungimea, lățimea și perimetrul sitului, dacă se știe că suprafața acestuia este de 612 m2.
Noțiuni de bază pentru afaceri, vom face mai întâi ecuația necesară. Fie x lățimea secțiunii, atunci lungimea ei va fi (x + 16). Din cele de mai sus rezultă că aria este determinată de expresia x (x + 16), care, conform condiției problemei noastre, este 612. Aceasta înseamnă că x (x + 16) = 612.
Soluția ecuațiilor quadratice complete, iar această expresie este exact așa, nu poate fi făcută prin metoda anterioară. De ce? Deși partea stângă a acestuia încă conține doi factori, produsul lor nu este deloc egal cu 0, deci alte metode sunt folosite aici.
discriminantă
Mai întâi de toate proizvedom modificările necesare, apoi apariția expresiei ar arata astfel: x2 + 16x - 612 = 0. Aceasta înseamnă că am primit expresia în forma corespunzătoare standardului de mai sus, unde a = 1, b = 16, c = -612.
Acesta poate fi un exemplu al soluției de ecuații patratice prin intermediul discriminatorului. Aici calculele necesare sunt efectuate conform schemei: D = b2 - 4ac. Această cantitate auxiliară nu numai că face posibilă găsirea cantităților necunoscute în ecuația de ordinul doi, ci determină numărul de variante posibile. În cazul în care D> 0, există două dintre ele, pentru D = 0 există o rădăcină. În cazul în care D<0, nu există șanse pentru rezolvarea ecuației.
Despre rădăcini și formula lor
În cazul nostru, discriminantul este: 256-4 (-612) = 2704. Aceasta indică faptul că există răspunsul la problema noastră. Dacă știm, de exemplu, discriminantul, soluția ecuațiilor patratice trebuie continuată cu aplicarea formulei de mai jos. Vă permite să calculați rădăcinile.

Aceasta înseamnă că în cazul prezentat: x1= 18, x2= -34. Un al doilea exemplu de realizare în această dilemă nu poate fi o soluție, deoarece dimensiunea porțiunii de teren nu poate fi măsurată în valori negative, atunci x (adică porțiunea lățime) este de 18 m De aceea vom calcula lungimea :. 18 + 16 = 34, iar perimetrul 2 (toatal de aproximativ 34 18) = 104 (m2).
Exemple și sarcini
Continuăm să studiem ecuațiile patratice. Exemple și soluții detaliate ale câtorva dintre ele vor fi date mai jos.
1) 15x2 + 20x + 5 = 12x2 + 27x + 1
Transferăm totul în partea stângă a ecuației, facem o transformare, adică obținem forma ecuației, care se numește standard, și o echivalează cu zero.
15x2 + 20x + 5 - 12x2 - 27x - 1 = 0
Adăugând acestea, definim discriminant: D = 49 - 48 = 1. Deci, ecuația noastră va avea două rădăcini. Le calculam conform formulei de mai sus, ceea ce înseamnă că prima dintre ele va fi de 4/3, iar cea de-a doua.
2) Acum rezolvați ghicitorii de altă natură.
Să aflăm dacă există rădăcini x2 - 4x + 5 = 1? Pentru a obține un răspuns exhaustiv, reducem polinomul la forma familiară corespunzătoare și calculează diferențiatul. În exemplul de mai sus, nu este necesar să se producă o ecuație patratică, deoarece esența problemei nu este deloc în acest sens. În acest caz, D = 16 - 20 = -4, ceea ce înseamnă că într-adevăr nu există nici o rădăcină.
Teorema lui Vieta
Este convenabil să se rezolve ecuațiile patratice prin formulele de mai sus și discriminant, atunci când rădăcina pătrată este extrasă din valoarea ultimului. Dar nu se întâmplă întotdeauna. Cu toate acestea, există multe modalități de a obține valorile variabilelor în acest caz. Exemplu: soluții de ecuații patratice de teorema lui Viet. Este numit în onoarea lui Francois Vieta, care a trăit în secolul al XVI-lea în Franța și a făcut o carieră strălucitoare datorită talentului și conexiunilor sale matematice în instanță. Puteți vedea portretul său în articol.

Modelul observat de celebrul francez a fost următorul. El a dovedit că rădăcinile ecuației din sumă sunt numeric egale cu -p = b / a, iar produsul lor corespunde q = c / a.
Acum, să analizăm anumite sarcini.
3x2 + 21x - 54 = 0
Pentru simplitate, traducem expresia:
x2 + 7x - 18 = 0
Folosim teorema lui Vieta, ceea ce ne va da următoarele: suma rădăcinilor este -7, iar produsul lor este -18. Prin urmare, constatăm că rădăcinile ecuației sunt numerele -9 și 2. face o verificare de fond, asigurați-vă că aceste variabile se potrivesc într-adevăr în expresie.
Graficul și ecuația parabolică
Conceptele funcției patratice și ecuațiile patrate sunt strâns legate. Exemple de acest lucru au fost deja date mai devreme. Acum ia în considerare unele puzzle-uri matematice un pic mai mult. Orice ecuație de tipul descris poate fi vizualizată. O dependență asemănătoare, desenată sub forma unui grafic, se numește parabolă. Diferitele sale tipuri sunt prezentate în figura de mai jos.

Orice parabola are un vârf, adică un punct din care ies ramurile. Dacă o> 0, ei merg în sus la infinit și când a<0, sunt trase în jos. Cel mai simplu exemplu de astfel de dependență este funcția y = x2. În acest caz, în ecuația x2= 0, necunoscutul poate avea doar o valoare, adică x = 0, ceea ce înseamnă că există doar o rădăcină. Acest lucru nu este surprinzător, deoarece aici D = 0, deoarece a = 1, b = 0, c = 0. Formula rădăcinii (mai precis, o rădăcină) a ecuației patrate este scrisă ca: x = -b / 2a.
Imaginile vizuale ale funcțiilor ajută la rezolvarea oricăror ecuații, inclusiv cele pătrate. Această metodă se numește grafică. Și valoarea variabilei x este coordonatele absciselor în punctele în care linia graficului se intersectează cu 0x. Coordonatele vârfului pot fi găsite din formula x0 = -b / 2a. Și înlocuind valoarea obținută în ecuația inițială a funcției, se poate găsi y0, adică cea de-a doua coordonată a vârfului parabolului, care aparține axei de coordonate.
Intersecția ramurilor parabolice cu axa abscisa
Există o mulțime de exemple cu soluția de ecuații patrate, dar există legi generale. Luați în considerare. Este clar că intersecția graficului cu axa 0x pentru a> 0 este posibilă numai dacă y0 ia valori negative. Și pentru a<0 coordonata y0 trebuie să fie pozitivă. Pentru variantele indicate D> 0. În caz contrar, D<0. Și când D = 0, vârful parabolei este situat direct pe axa 0x.
Conform parcelei parabolei, se pot determina și rădăcinile. Converse este, de asemenea, adevărat. Asta este, dacă aveți o reprezentare vizuală a unei funcții pătratică nu este ușor, poate fi asimilată cu partea dreaptă a expresiei la 0 și de a rezolva ecuația rezultată. Și cunoscând punctul de intersecție cu axa 0x, este mai ușor să trasați graficul.
Din istorie
Folosind ecuațiile ce conțin variabile, crescute într-un pătrat pe vremuri, nu doar calcule matematice și suprafață măsurată de forme geometrice. Calcule similare au fost nevoie vechi pentru marile descoperiri în fizică și astronomie, precum și pentru elaborarea de prognoze astrologice.

După cum presupun oamenii de știință moderni, una dintre primele soluții de ecuații patratice a fost ocupată de locuitorii Babilonului. Sa întâmplat cu patru secole înainte de debutul erei noastre. Desigur, calculele lor diferă radical de cele care au fost adoptate acum și s-au dovedit a fi mult mai primitive. De exemplu, matematicienii mezopotamieni nu aveau idee despre existența unor numere negative. În plus față de ele erau și alte subtilități din cele pe care le știe orice elev școlar din prezent.
Poate chiar și oamenii de știință anterioare soluție Babilon de ecuații pătratice angajat salvie din India Baudhayama. Sa întâmplat cam opt secole înainte de debutul erei lui Hristos. Adevăratele ecuații de ordinul doi, metodele de rezolvare pe care le-a citat, au fost cele mai simple. În plus, matematicienii chinezi au fost interesați de întrebări similare în zilele vechi. În Europa, am început să rezolve ecuații pătratice doar la începutul secolului al XIII-lea, dar mai târziu au fost folosite în lucrările sale astfel de oameni de știință, cum ar fi Newton, Descartes și multe altele.
 Unde se aplică metoda cu cele mai mici pătrate
Unde se aplică metoda cu cele mai mici pătrate Logaritme: exemple și soluții
Logaritme: exemple și soluții Fundamentele teoretice ale Ingineriei Electrice: Metoda Stresului Nodal
Fundamentele teoretice ale Ingineriei Electrice: Metoda Stresului Nodal Metoda elementului finit este un mod universal de rezolvare a ecuațiilor diferențiale
Metoda elementului finit este un mod universal de rezolvare a ecuațiilor diferențiale Metoda Seidel-Gauss. Metoda internațională
Metoda Seidel-Gauss. Metoda internațională Proprietățile și căile de căutare a rădăcinilor ecuației patrate
Proprietățile și căile de căutare a rădăcinilor ecuației patrate Ce este egalitatea? Primul semn și principiile egalității
Ce este egalitatea? Primul semn și principiile egalității Ecuația - ce este? Definiția termenului, exemple
Ecuația - ce este? Definiția termenului, exemple Sisteme de ecuații algebrice liniare. Sisteme omogene de ecuații algebrice liniare
Sisteme de ecuații algebrice liniare. Sisteme omogene de ecuații algebrice liniare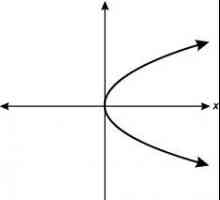 Care sunt zerourile unei funcții și cum să le definiți?
Care sunt zerourile unei funcții și cum să le definiți? Exemple de sisteme de ecuații liniare: metoda de rezolvare
Exemple de sisteme de ecuații liniare: metoda de rezolvare Metoda lui Cramer și aplicarea acestuia
Metoda lui Cramer și aplicarea acestuia Ecuații liniare cu una și două variabile, inegalități liniare
Ecuații liniare cu una și două variabile, inegalități liniare Soluția ecuațiilor liniare
Soluția ecuațiilor liniare Ecuațiile iraționale și modalitățile de a le rezolva
Ecuațiile iraționale și modalitățile de a le rezolva Programarea liniară
Programarea liniară Metoda dichotomiei
Metoda dichotomiei Ecuații diferențiale - Informații generale și domeniu de aplicare
Ecuații diferențiale - Informații generale și domeniu de aplicare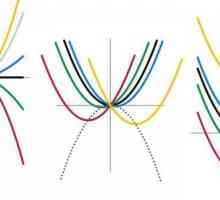 Rezolvarea ecuatiilor patrate si construirea de grafice
Rezolvarea ecuatiilor patrate si construirea de grafice Rădăcina ecuației este informația de familiarizare
Rădăcina ecuației este informația de familiarizare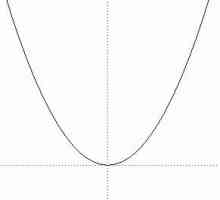 Cum să găsiți vârful unei parabole și să o construiți
Cum să găsiți vârful unei parabole și să o construiți
 Logaritme: exemple și soluții
Logaritme: exemple și soluții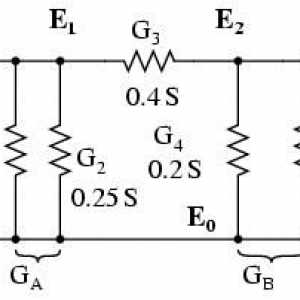 Fundamentele teoretice ale Ingineriei Electrice: Metoda Stresului Nodal
Fundamentele teoretice ale Ingineriei Electrice: Metoda Stresului Nodal Metoda elementului finit este un mod universal de rezolvare a ecuațiilor diferențiale
Metoda elementului finit este un mod universal de rezolvare a ecuațiilor diferențiale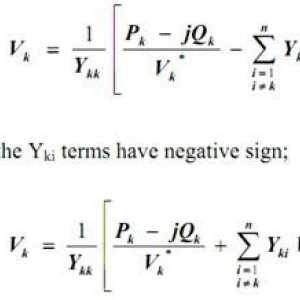 Metoda Seidel-Gauss. Metoda internațională
Metoda Seidel-Gauss. Metoda internațională Proprietățile și căile de căutare a rădăcinilor ecuației patrate
Proprietățile și căile de căutare a rădăcinilor ecuației patrate Ce este egalitatea? Primul semn și principiile egalității
Ce este egalitatea? Primul semn și principiile egalității Ecuația - ce este? Definiția termenului, exemple
Ecuația - ce este? Definiția termenului, exemple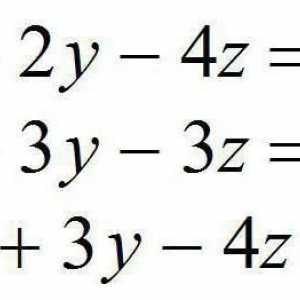 Sisteme de ecuații algebrice liniare. Sisteme omogene de ecuații algebrice liniare
Sisteme de ecuații algebrice liniare. Sisteme omogene de ecuații algebrice liniare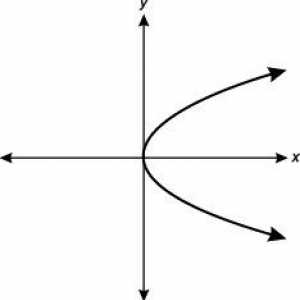 Care sunt zerourile unei funcții și cum să le definiți?
Care sunt zerourile unei funcții și cum să le definiți? Exemple de sisteme de ecuații liniare: metoda de rezolvare
Exemple de sisteme de ecuații liniare: metoda de rezolvare