Exemple de sisteme de ecuații liniare: metoda de rezolvare
Sistemele de ecuații au fost utilizate pe scară largă în domeniul economic în modelarea matematică a diferitelor procese. De exemplu, atunci când rezolvăm sarcini de management și planificarea producției, rute logistice (sarcina de transport) sau plasarea echipamentelor.
conținut
- Ecuația liniară
- Tipuri de sisteme de ecuații liniare
- Metode simple și complexe pentru rezolvarea sistemelor de ecuații
- Soluționarea sistemelor prin înlocuire
- Soluție prin adăugarea algebrică
- Metoda de rezolvare prin introducerea unei noi variabile
- O metodă vizuală pentru rezolvarea sistemelor
- Matricea și variantele sale
- Regulile pentru transformarea unui sistem de ecuații într-o matrice
- Variantele de găsire a matricei inverse
- Soluția exemplelor de sisteme de ecuații liniare prin metoda matricei
- Soluția sistemelor prin metoda gauss
Sistemele de ecuații sunt utilizate nu numai în domeniul matematicii, ci și în fizică, chimie și biologie, în rezolvarea problemelor legate de găsirea mărimii populației.

Un sistem de ecuații liniare este două sau mai multe ecuații cu mai multe variabile, pentru care este necesară găsirea unei soluții generale. O astfel de secvență de numere pentru care toate ecuațiile devin realități egale sau dovedesc că secvența nu există.
Ecuația liniară
Ecuațiile formelor ax + by = c sunt numite liniare. Notația x, y este necunoscută, valoarea căreia trebuie să fie găsită, b, a sunt coeficienții variabilelor, c este termenul liber al ecuației.
Soluția ecuației prin construirea graficului său va avea forma unei linii drepte, toate ale căror puncte sunt o soluție a polinomului.
Tipuri de sisteme de ecuații liniare
Cele mai simple exemple sunt sistemele de ecuații liniare cu două variabile X și Y.
F1 (x, y) = 0 și F2 (x, y) = 0, unde F1,2 sunt funcții și (x, y) sunt variabile de funcție.
Rezolvați sistemul de ecuații - aceasta înseamnă găsirea valorilor (x, y) la care sistemul se transformă în egalitatea corectă sau stabilind că nu există valori potrivite x și y.
O pereche de valori (x, y), scrise sub forma coordonatelor unui punct, se numeste solutia unui sistem de ecuatii liniare.
Dacă sistemele nu au o soluție comună sau soluții nu există, ele sunt numite echivalente.
Sistemele omogene de ecuații liniare sunt sisteme a căror parte dreaptă este egală cu zero. Dacă dreptul după semnul "egalității" are o valoare sau este exprimat printr-o funcție, un astfel de sistem nu este omogen.
Numărul de variabile poate fi mult mai mare decât două, atunci ar trebui să vorbim despre un exemplu de sistem de ecuații liniare cu trei sau mai multe variabile.
Confruntate cu sisteme, elevii presupun că numărul de ecuații trebuie să coincidă în mod necesar cu numărul de necunoscuți, dar acest lucru nu este valabil. Numărul de ecuații din sistem nu depinde de variabile, pot exista cât de mult vor ei.
Metode simple și complexe pentru rezolvarea sistemelor de ecuații
Nu există o metodă analitică generală pentru rezolvarea unor astfel de sisteme, toate metodele se bazează pe soluții numerice. În cursul școlar al matematicii, sunt descrise în detaliu metode precum permutarea, adăugarea algebrică, substituția, precum și metoda grafică și matricea, soluția Gauss.
Principala sarcină în predarea metodelor de rezolvare este să vă învăț cum să analizați corect sistemul și să găsiți algoritmul optim pentru fiecare exemplu. Principalul lucru nu este să memorezi sistemul de reguli și acțiuni pentru fiecare metodă, ci să înțelegi principiile aplicării acestei sau acelei metode
Soluția exemplelor de sisteme de ecuații liniare din clasa a 7-aa programului general de școală este destul de simplă și explicată în detaliu. În orice matematică manuală, se acordă o atenție suficientă acestei secțiuni. Soluția exemplelor de sisteme de ecuații liniare prin metoda Gauss și Kramer este studiată mai detaliat la primele cursuri ale instituțiilor de învățământ superior.
Soluționarea sistemelor prin înlocuire
Acțiunile metodei de substituție vizează exprimarea valorii unei variabile prin cea de a doua. Expresia este substituită în ecuația rămasă, apoi este adusă la forma cu o variabilă. Acțiunea se repetă în funcție de numărul de necunoscute din sistem
Oferim o soluție a unui exemplu de sistem de ecuații liniare din clasa a 7-a prin metoda substituției:

Așa cum se poate vedea din exemplu, variabila x a fost exprimată în termeni de F (X) = 7 + Y. Expresia rezultată, substituită în a doua ecuație a sistemului în locul lui X, a ajutat la obținerea unei variabile Y în a doua ecuație. Soluția din acest exemplu nu cauzează dificultăți și vă permite să obțineți valoarea lui Y. Ultimul pas este să verificați valorile obținute.
Rezolvarea exemplului unui sistem de ecuații liniare prin substituire nu este întotdeauna posibilă. Ecuațiile pot fi complexe, iar exprimarea variabilei prin cel de-al doilea necunoscut se va dovedi prea greoaie pentru calcule ulterioare. În cazul în care există mai mult de 3 necunoscute în sistem, înlocuirea este, de asemenea, inadmisibilă.
Soluția unui exemplu al unui sistem de ecuații liniare neomogene:

Soluție prin adăugarea algebrică
Atunci când se caută soluția sistemelor prin metoda adiției, se efectuează adunarea pe termen lung și multiplicarea ecuațiilor prin numere diferite. Scopul final al acțiunilor matematice este o ecuație cu o variabilă.

Practica și observarea sunt necesare pentru aplicarea acestei metode. Rezolvarea sistemului de ecuații liniare prin metoda adiției pentru un număr de variabile de 3 sau mai multe nu este ușor. Adăugarea algebrică este convenabilă când fracțiile și zecimalele sunt prezente în ecuații.
Soluție algoritm:
- Multiplicați ambele părți ale ecuației cu un anumit număr. Ca rezultat al operării aritmetice, unul dintre coeficienții variabilei ar trebui să devină egal cu 1.
- În cele din urmă, adăugați expresia rezultată și găsiți una dintre cele necunoscute.
- Înlocuiți această valoare în a doua ecuație a sistemului pentru a găsi variabila rămasă.
Metoda de rezolvare prin introducerea unei noi variabile
O nouă variabilă poate fi introdusă dacă în sistem este necesară găsirea unei soluții pentru nu mai mult de două ecuații, numărul de necunoscute nu trebuie să fie mai mare de două.
Metoda este utilizată pentru a simplifica una dintre ecuații prin introducerea unei noi variabile. Noua ecuație este rezolvată în raport cu necunoscutul, iar valoarea obținută este utilizată pentru a determina variabila inițială.

Se vede din exemplu că prin introducerea unei noi variabile t, a fost posibilă reducerea primei ecuații a sistemului la trinomul cuadratural standard. Rezolvați polinomul prin găsirea discernământului.
Este necesar să se găsească valoarea discriminant prin formula cunoscută: D = b2 - 4 * a * c, în cazul în care D - multiplicatoare polinomial - discriminant, b, a, c dorit. În exemplul dat, a = 1, b = 16, c = 39, prin urmare, D = 100. Dacă discriminante este mai mare decât zero, atunci cele două soluții: t = -b ± Radic-D / 2 * o, în cazul în care discriminant este mai mică decât zero, atunci o singură soluție: x = -b / 2 * a.
Soluția pentru sistemele rezultate este găsită prin metoda de adăugare.
O metodă vizuală pentru rezolvarea sistemelor
Potrivit pentru sisteme cu 3 ecuații. Metoda constă în reprezentarea pe axa de coordonate a graficelor fiecărei ecuații care intră în sistem. Coordonatele punctelor de intersecție a curbelor u vor fi soluția generală a sistemului.
Metoda grafică are un număr de nuanțe. Să luăm în considerare câteva exemple de rezolvare a sistemelor de ecuații liniare într-un mod vizual.

După cum puteți vedea din exemplu, au fost construite două puncte pentru fiecare linie, valorile variabilei x au fost alese arbitrar: 0 și 3. Pe baza valorilor lui x s-au găsit valorile pentru y: 3 și 0. Punctele cu coordonatele (0, 3) și (3, 0) au fost marcate pe grafic și conectate printr-o linie.
Acțiunea trebuie repetată pentru a doua ecuație. Punctul de intersecție a liniilor este o soluție a sistemului.
În exemplul următor, trebuie să găsim o soluție grafică a sistemului de ecuații liniare: 0.5x-y + 2 = 0 și 0.5x-y-1 = 0.

După cum puteți vedea din exemplu, sistemul nu are o soluție, deoarece graficele sunt paralele și nu se intersectează pe toată lungimea lor.

Sistemele din Exemplele 2 și 3 sunt similare, însă în construcții devine evident că soluțiile lor sunt diferite. Trebuie reținut că nu este întotdeauna posibil să se spună dacă sistemul are sau nu o soluție, este întotdeauna necesar să se construiască un program.
Matricea și variantele sale
Matricele sunt folosite pentru a înregistra pe scurt un sistem de ecuații liniare. Matricea se numește o masă de un tip special, plină cu numere. Matricea formei n * m are n - rânduri și m - coloane.
Matricea este pătrată atunci când numărul de coloane și rânduri este egal unul cu celălalt. Un vector de matrice este o matrice de o coloană cu un număr infinit de rânduri. O matrice cu una pe una dintre diagonale și alte elemente zero este numită matrice unitate.
O matrice inversă este o astfel de matrice, înmulțită cu care matricea inițială se transformă într-o singură matrice, o astfel de matrice există numai pentru matricea pătrată originală.
Regulile pentru transformarea unui sistem de ecuații într-o matrice
În ceea ce privește sistemele de ecuații, coeficienții și termenii liberi ai ecuațiilor sunt scrise ca numere ale matricei, o ecuație este un rând al matricei.
Un rând de matrice se spune că este nenul, dacă cel puțin un element al șirului nu este zero. Prin urmare, dacă în oricare dintre ecuații numărul de variabile este diferit, atunci este necesar să se scrie zero la locul necunoscutului necunoscut.
Coloanele coloanelor trebuie să corespundă strict variabilelor. Aceasta înseamnă că coeficienții variabilei x pot fi scrise doar într-o singură coloană, de exemplu, primul, coeficientul necunoscut y este numai în a doua coloană.
Atunci când matricea este înmulțită, toate elementele matricei sunt înmulțite consecutiv cu un număr.
Variantele de găsire a matricei inverse
Formula pentru găsirea matricei inverse este destul de simplă: K-1= 1 / | K |, unde K-1 - matricea inversă și | K | determinant matricial. | K | nu ar trebui să fie zero, atunci sistemul are o soluție.
Determinantul poate fi calculat cu ușurință pentru o matrice de două până la două, fiind necesară numai multiplicarea diagonală a elementelor. Pentru varianta "trei cu trei", formula | K | = a1b2c3 + o1b3c2 + o3b1c2 + o2b3c1 + o2b1c3 + o3b2c1. Puteți utiliza formula, dar vă puteți aminti că trebuie să luați un element din fiecare rând și din fiecare coloană, astfel încât numărul de coloane și rânduri de elemente să nu fie repetat în lucrare.
Soluția exemplelor de sisteme de ecuații liniare prin metoda matricei
O metodă matricială de căutare a unei soluții face posibilă reducerea înregistrărilor greoaie atunci când se rezolvă sisteme cu un număr mare de variabile și ecuații.

În exemplul anm - coeficienți de ecuații, matrice - vector xn - variabile și bn - membrii liberi.

Apoi, trebuie să găsim matricea inversă și să o înmulțim cu matricea originală. Găsirea valorilor variabilelor în matricea unității rezultate este o sarcină ușor de executat.

Soluția sistemelor prin metoda Gauss
În matematica superioară, metoda Gauss este studiată împreună cu metoda Cramer, iar procesul de găsire a soluțiilor la sisteme este numit și metoda Gauss-Cramer. Aceste metode se utilizează atunci când se găsesc sisteme variabile cu un număr mare de ecuații liniare.
Metoda Gaussiană este foarte asemănătoare cu soluțiile care utilizează permutări și adăugarea algebrică, dar este mai sistematică. În cursul școlii, metoda Gauss este folosită pentru sistemele de 3 și 4 ecuații. Scopul metodei este de a aduce sistemul în formă de trapez inversat. Prin transformări și substituții algebrice, valoarea uneia dintre variabile se găsește într-una din ecuațiile sistemului. A doua ecuație este o expresie cu 2 necunoscute, bine, 3 și respectiv 4, cu 3 și 4 variabile.
După reducerea sistemului la forma descrisă, soluția ulterioară este redusă la înlocuirea succesivă a variabilelor cunoscute în ecuațiile sistemului.
În manualele școlare pentru gradul 7, un exemplu de soluție prin metoda Gauss este descris după cum urmează:

După cum se poate vedea din exemplu, în etapa (3) două ecuații 3x3-2x4= 11 și 3x3+2x4= 7. Soluția oricărei ecuații va permite cunoașterea uneia dintre variabilele xn.

Teorema 5, menționată în text, precizează că dacă una dintre ecuațiile sistemului este înlocuită cu una echivalentă, atunci sistemul rezultat va fi, de asemenea, echivalent cu cel original.
Metoda lui Gauss este dificilă pentru elevii din școala secundară, dar este una dintre cele mai interesante modalități de a dezvolta priceperea copiilor care studiază în cadrul programului de studiu aprofundat în clasele matematice și fizice.
Pentru simplitate, este obișnuit să se scrie calcule după cum urmează:

Coeficienții ecuațiilor și termenii liberi sunt scrise sub forma unei matrici, în care fiecare rând al matricei este legat de una din ecuațiile sistemului. Linie verticală separă partea stângă a ecuației din dreapta. Numerele romane denotă numărul de ecuații din sistem.
Mai întâi, scrieți matricea din care să lucrați, apoi toate acțiunile efectuate cu una dintre linii. Matricea obținută este scrisă după semnul "săgeată" și continuă să efectueze acțiunile algebrice necesare până când rezultatul este obținut.
Ca urmare, matricea trebuie să se întoarcă în care una dintre diagonalele sunt în valoare de 1, și toți ceilalți factori sunt egale cu zero, adică matricea este redusă la o singură minte. Nu trebuie să uităm să efectuăm calcule cu cifrele ambelor părți ale ecuației.
Această metodă de înregistrare este mai puțin greoaie și permite să nu fie distrasă de enumerarea a numeroase necunoscute.
Aplicarea gratuită a oricărei metode de soluționare va necesita îngrijire și o anumită experiență. Nu toate metodele au o natură aplicată. Unele modalități de găsire a soluțiilor sunt mai preferabile în cealaltă zonă a activității umane, în timp ce altele există în scopul instruirii.
 Metoda elementului finit este un mod universal de rezolvare a ecuațiilor diferențiale
Metoda elementului finit este un mod universal de rezolvare a ecuațiilor diferențiale Metoda Seidel-Gauss. Metoda internațională
Metoda Seidel-Gauss. Metoda internațională Proprietățile și căile de căutare a rădăcinilor ecuației patrate
Proprietățile și căile de căutare a rădăcinilor ecuației patrate Ecuația - ce este? Definiția termenului, exemple
Ecuația - ce este? Definiția termenului, exemple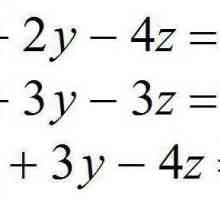 Sisteme de ecuații algebrice liniare. Sisteme omogene de ecuații algebrice liniare
Sisteme de ecuații algebrice liniare. Sisteme omogene de ecuații algebrice liniare Care sunt zerourile unei funcții și cum să le definiți?
Care sunt zerourile unei funcții și cum să le definiți? Ecuația de regresie
Ecuația de regresie Ecuațiile chimice: cum să rezolve cel mai eficient
Ecuațiile chimice: cum să rezolve cel mai eficient Teorema Vieta și o istorie
Teorema Vieta și o istorie Ecuații ecuații egale - exemple cu soluții, singularități și formule
Ecuații ecuații egale - exemple cu soluții, singularități și formule Metoda lui Cramer și aplicarea acestuia
Metoda lui Cramer și aplicarea acestuia Ecuații liniare cu una și două variabile, inegalități liniare
Ecuații liniare cu una și două variabile, inegalități liniare Soluția ecuațiilor liniare
Soluția ecuațiilor liniare Programarea liniară
Programarea liniară Metoda dichotomiei
Metoda dichotomiei Metoda Gauss: exemple de soluții și cazuri speciale
Metoda Gauss: exemple de soluții și cazuri speciale Metoda simplă de iterație pentru rezolvarea sistemelor de ecuații liniare (SLAE)
Metoda simplă de iterație pentru rezolvarea sistemelor de ecuații liniare (SLAE) Ecuații diferențiale - Informații generale și domeniu de aplicare
Ecuații diferențiale - Informații generale și domeniu de aplicare Rezolvarea ecuatiilor patrate si construirea de grafice
Rezolvarea ecuatiilor patrate si construirea de grafice Rădăcina ecuației este informația de familiarizare
Rădăcina ecuației este informația de familiarizare Cum să găsiți vârful unei parabole și să o construiți
Cum să găsiți vârful unei parabole și să o construiți
 Metoda Seidel-Gauss. Metoda internațională
Metoda Seidel-Gauss. Metoda internațională Proprietățile și căile de căutare a rădăcinilor ecuației patrate
Proprietățile și căile de căutare a rădăcinilor ecuației patrate Ecuația - ce este? Definiția termenului, exemple
Ecuația - ce este? Definiția termenului, exemple Sisteme de ecuații algebrice liniare. Sisteme omogene de ecuații algebrice liniare
Sisteme de ecuații algebrice liniare. Sisteme omogene de ecuații algebrice liniare Care sunt zerourile unei funcții și cum să le definiți?
Care sunt zerourile unei funcții și cum să le definiți? Ecuațiile chimice: cum să rezolve cel mai eficient
Ecuațiile chimice: cum să rezolve cel mai eficient Ecuații ecuații egale - exemple cu soluții, singularități și formule
Ecuații ecuații egale - exemple cu soluții, singularități și formule